美国高考数学题（大家热议的美国数学高考题）

美国高考数学题（大家热议的美国数学高考题）

之前曾把下面这网道美国数学高考题发到今日头条，没想到竟然获得了25万展现和858条留言。前几天我在指出《隐秘的角落》里关于张东升所画的错误心形线的文章里，也谈到了这个问题，结果同样引起了不少人的讨论。现在，该是给这个问题一个交代的时候了。

问题是这样的：

小圆的半径是大圆的1/3，大圆固定不动，小圆绕大圆滚一圈回到原位，请问小圆自己转了几圈？

这个问题的正确答案为4圈。为什么30万人只有3人答对了，原因就在于正确答案并未出现在选项中。出题人着实把大家坑了一把。事实上，这个问题也被称为“硬币悖论”， 也就是结果与人们的直觉认知相悖。

对于这一问题，许多人认为答案就应该是3圈，因为大圆周长就是小圆的3倍。给出4圈这一正确答案的，其解释也是五花八门，下面我对一些主要的答案逐一解释。

1. 自转公转论

小圆自转3圈，绕着大圆公转1圈，一共转了4圈。

这一答案堪称最具欺骗性解答。听上去似乎很有道理，4圈的答案也对，还能傍上地球自转和公转的理论。呃，大家都这么说，那我也假装自己懂了吧。回答4圈的人中估摸有一多半人是这么想的，其实根本没有深入去思考。

真的是这样吗？我们再来看看这个问题问的是什么？

题目问的是小圆自己转了多少圈，就是小圆绕着自己的中心转了几圈，这就是自转的概念。如果说自转3圈，那答案就应该是3圈才对。公转讲的是小圆绕着大圆的中心转，跟自转无关。实际上，小圆即便不自转，也可以绕着大圆的中心公转一圈。在这个问题里，小圆确实绕大圆公转了1圈，但这跟小圆自转几圈没有关系。因为，小圆自转就有4圈。也就是说，小圆自转了4圈，公转了1圈。

2. 圆心轨迹法

小圆的圆心运动轨迹也是个圆，其半径为4r，所以走过的长度为8r。小圆每自转一圈圆心走过2r，因此转了4圈。

如果是小圆在平地上滚，确实每走过2r就是绕着圆心转一圈。

但到绕着大圆网滚这个问题里，首先得证明圆心走过2r的长度，小圆绕着圆心转了360这个结论。即如下图所示，小圆圆心走过2r的距离，恰好走过小圆圆心所在圆周长的1/4，为什么此时小圆正好绕着自己的圆心转了一圈？没有证明过程，网直接拿平地的结论搬过来是不严谨的。

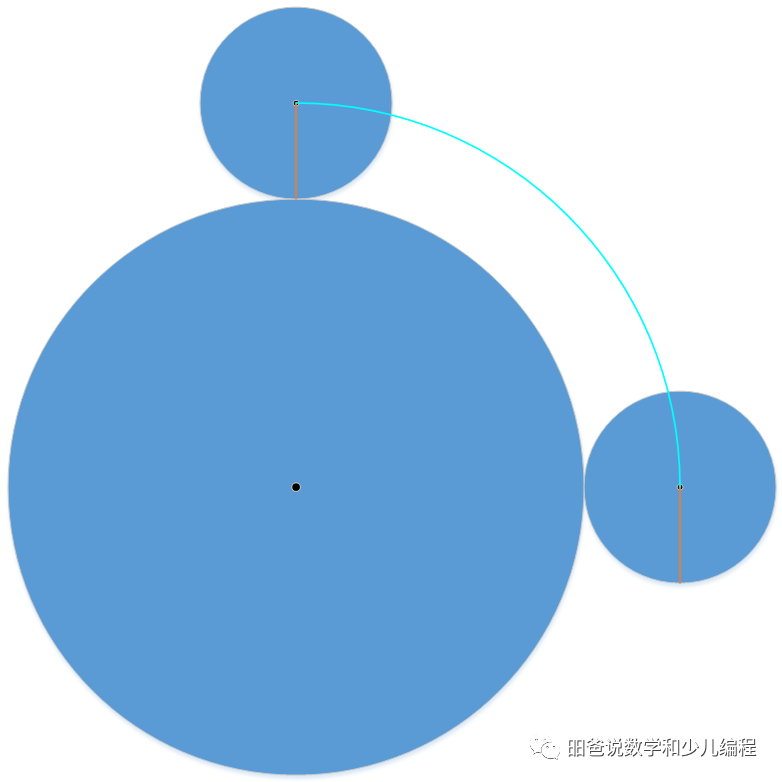
还有人说小圆上每个点走过的长度等于小圆圆心走的长度，所以如此。这个结论就不对了，后面再讲。

3. 质点法

质点法类似于圆心轨迹法。即把小圆看成一个质点，从而小圆的运动轨迹是一个半径为4r的圆，质点一共走了8r的长度，每走2r的长度绕圆心转一圈，所以转了4圈。这个方法首先得理解什么是质点，其次，与圆心轨迹法一样，也需要证明一个之前的那个小结论才行。

4. 相对运动法

小圆和大圆如果各自固定圆心，类似于齿轮一样同时转动，那么小圆顺时针转3圈，大圆逆时针转1圈，小圆相对于大圆转了4圈。现在大圆固定不动，小圆需要相对于大圆转4圈才行。这个解释是可以的，但相对运动对于大部分人（特别是孩子）而言，还是太过于抽象了。

那么，有没有一种比较直观的解释呢？我下面给出的方法是纯粹从数学几何关系来解释的，学过角度和圆周长的小学高年级学生应该都能理解。

5. 纯几何方法

这个问题里有一点是确定的，即小圆的周长是大圆的1/3。小圆在大圆上滚过2r的长度即1/3大圆的周长，滚到了如下图所示的位置，此时小圆绕着自己的圆心转了360+120=480。小圆贴着大圆滚6r的长度正好滚回原点，此时转了4803=1440。1440360=4圈。

6. 心形线的长度

刚才提到，在第二种方法中，有人认为小圆上任何一点走过的长度与圆心走过的长度是一样的，真的是这样吗？

不妨再看一下类似的但更简单一点的心形线，也就是两个圆的半径一样时的情况。在之前《隐藏在《隐秘的角落》里的错误心形线》这篇文章中，给出了心形线的极坐标方程表示。

此时，由极坐标方程r=2a(1-cos)和微积分可以求得心形线的长度为16a（具体计算过程如下），而小圆圆心走的轨迹是一个半径为2a的圆，因此走的长度为4a。也就是说，在这种滚动的问题里，圆心走过的长度和圆上任意一点走过的长度是不一样的。

如果你有幼儿园到初中的学龄娃，想加入数学讨论群的，可以留言并告知年级。